컴퓨터 그래픽스 공부 - 2(1)
선형대수학의 기초
m 개의 행과 n 개의 열이 있으면 m * n 행렬의 사이즈를 구하는 방법
만약 m개의 행과 n 개의 열이 같으면 ( m = n ) 정사각 행렬이라고 한다. (square matrix)
두 가지 행렬이 주어졌을 때

첫 번째 첫 번째 행과 첫 번째 열을 쌍으로 곱하면 원소가 만들어진다.
ex ) (a11 a12) * (b11 b21) = (a11b11 + a12b21)
a행렬의 크기를 L * M이라고 하고 b 행렬의 크기를 M * N이라고 했을 때, 두 개의 행렬 중 M이 공통되므로 곱셈이 가능해진다.
결과로 나오는 행렬의 크기는 남은 L * N이 된다.
2차원 백터 ( x, y ) 3차원 벡터 (x, y, z)들을 대부분 low vector라고 표현한다.
좌표를 열의 형태로 쓸 수 있는데 이것을 column vector라고 말한다.


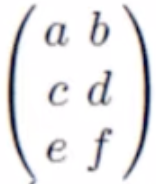
2by1 * 3by2 = 3by2 행렬이 나온다. (2가 공통적으로 포함되기 때문에 곱셈이 가능해진다.)
또한 행렬의 행과 열을 바꿔 놓은 것은 전치행렬(transpose)이라고 한다. 3 * 2 행렬의 행과 열을 바꿔놓으면 다음 사진과 같이 변환된다.

행렬과 벡터의 곱셈은 위 방식 말고 행벡터를 왼쪽으로 놓는 방식으로 표현할 수 도 있다.

OpenGL에서는 열벡터를 사용하고 ( 오른쪽에 벡터 ) Direct3D 에서는 행벡터를 사용한다. ( 왼쪽 벡터)
단위행렬 ( identity matrix )은 정사각행렬 중, 대각선에 놓인 원소들의 값이 모두 1이고 나머지 원소의 값은 0인 경우를 말한다.

또한 어떠한 무작위 행렬(M)과 단위행렬(I)의 곱셈은
MI = IM = M 즉 어떤 행렬과 곱하던 그 행렬을 유지한다.
정사각행렬 A와 B를 곱하여 I 라는 결과가 된다면 , A*B = I 라면 B는 A의 역행렬이라고 표현한다.
A^-1 승으로 표현할 수 있으며, 이와 같은 개념으로 B*A = I 라면 A는 B의 역행렬 B ^-1승으로 표현할 수 있다.
2차원 벡터 V의 좌표를 (Vx, Vy)로 표현할 때, V의 길이는 루트 Vx^2 + Vy^2로 정의되며 ||V|| 으로 표기된다.
3차원 벡터의 길이는 루트 Vx^2 + Vy^2 + Vz^2가 된다.
V(벡터)를 ||V||(벡터길이)로 나누는 과정을 정규화 ( normalization )이라고 하는데 ,
단위 벡터(unit vecetor)란 = V(벡터) / ||V|| (벡터길이)는 V(벡터)와 같은 방향을 가지면서 길이가 1 인 벡터이다.